Les mathématiques augmentées
un concept novateur
Plus de quatre décennies après la sortie des premiers PC, faute d'outils logiciels adéquats, l’interactivité des exercices de mathématiques créés par l'enseignant est toujours limitée aux QCM, textes à trous, glisser-déposer et certains types prédéfinis.
Les mathématiques augmentées sont une création française qui offre au professeur de mathématiques le moyen de rendre interactifs ses exercices classiques, de créer son propre contenu numérique sans se limiter aux QCM ou à d'autres types de questions prédéfinies et de personnaliser les corrigés fournis par les éditeurs sans limite. Les exercices et leurs corrigés fournis par l’éditeur même avec des données aléatoires peuvent être personnalisés par l’enseignant sans limitation pour les adapter à sa pédagogie : modifications, explications, étapes et présentations des calculs.
Les mathématiques augmentées permettent aux enseignants de dépasser les QCM. Ce nouveau concept est mis en œuvre avec des exercices d'un nouveau type adapté au numérique et avec une application Android.
Éditeurs, enseignants, acteurs du numérique éducatif, vous êtes intéressés ? Écrivez-nous.
La mise en oeuvre textuelle des mathématiques augmentées sous la forme d'exercices, protégée par le droit d'auteur est déposée à l'INPI. La structure de la base de données d'exercices, ainsi que la mise en oeuvre logicielle sous forme de programme, du concept, sont enregistrées à l'APP et sont protegées par le droit d'auteur comme œuvres originales. D'autres lois protègent notre oeuvre.
Les mathématiques augmentées par des exemples
Dans vos corrigés, vous pouvez intéger des rappels de cours, des commentaires et toute explication que vous donnez en classe sans aucune limite.
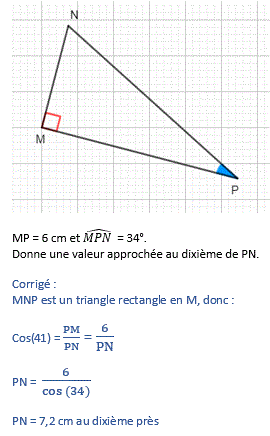
Soit à calculer le côté d'un triangle rectangle. Ici l'énoncé comprend une figure.
Si les nombres de l'énoncé générés de manière pseudo-aléatoire sont 6 et 34 alors l'élève verra l'énoncé et le corrigé (après avoir saisi sa réponse) que vous avez modifiés et qui peuvent prendre la forme suivante :
Soit à développer (3x + 4)² avec 3 et 4 deux nombres pseudo-aléatoires.
- Vous pouvez exiger une expression ordonnée 9x² + 24x + 16.
- Vous pouvez aussi accepter toute expression équivalente composée des 3 termes 9x², 24x et 16 comme 24x + 9x² + 16.
Soit à calculer
- L'expression numérique 2 + 3 x 4 (2, 3 et 4 sont des nombres pseudo-aléatoires).
- Si vous préférez présenter les calculs en une seule ligne vous mettrez dans votre corrigé
3 + 2 x 4 = 3 + 8 = 11 - Si vous préférez écrire une ligne par étape vous mettrez
2 x 4 = 8
3 + 8 = 11 - Par exemple, vous pouvez inclure dans le corrigé "On effectue d'abord 2 x 4 car la multiplication est prioritaire sur l'addition" bien que les nombres 2 et 4 soient pseudo-aléatoires. Le contenu de cette phrase va changer et les nombres 2 et 4 seront remplacés par les nouveaux nombres générés à la répétition de la question lors de l'entraînement de l'élève.
- Les nombres 2, 3 et 4 sont des nombres pseudo-aléatoires obtenus suivant des critères que vous fixez : minimum, maximum et nombre de décimales.
Soit à comparer 2 nombres pseudo-aléatoires avec la même partie entière 7,3 et 7,29.
- Vous pouvez rajouter des zéros inutiles à 7,3 qui devient 7,30 dans votre corrigé affiché à l'élève pour conclure et écrire dans le corrigé qu'un zéro inutile est rajouté. Si les deux nombres générés sont 7,3 et 7,291 vous pouvez précisez que ce sont deux zéros inutiles qui sont rajoutés pour comparer 7,300 et 7,291.
Les explications que vous donnez dans un corrigé peuvent être ciblées et très proches des explications que vous donnez oralement en classe. - Vous pouvez aussi extraire les chiffres des dixièmes 3 et 2 dans votre corrigé si vous n'utilisez pas les zéros inutiles pour expliquer la comparaison.
Soit à multiplier un nombre par 100. Vous pouvez choisir de rappeler le cours dans le corrigé ou choisir une formulation adaptée au nombre à multiplier comme vous faites en classe. Voici des formulations modifiables adaptées à la valeur du nombre pseudo-aléatoire généré :
- 78 x 100 = 7800
Multiplier un nombre entier par 100 revient à rajouter deux zéros à droite. - 2,768 x 100 = 276,8
Multiplier un nombre à virgule par 100 revient à déplacer la virgule de 2 positions vers la droite. - 3,9 x 100 = 390
Multiplier un nombre à virgule par 100 revient à déplacer la virgule de 2 positions vers la droite.
Ici un zéro inutile est rajouté à droite et 3,9 devient 3,90 pour déplacer la virgule de 2 positions.
Vous avez une question ? écrivez-nous.
Dans la même question répétée pendant l'entraînement, si les nombres générés sont par exemple 4 et 41 alors l'énoncé et le corrigé seront :
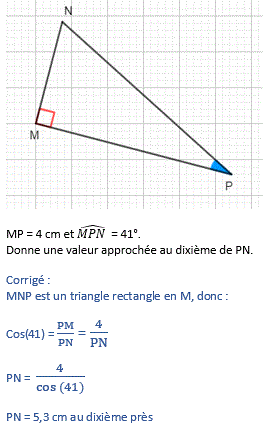
Ansi, le contenu numérique que vous proposez à vos élèves est de même qualité pédagogique que votre contenu classique.
Offrez à vos élèves un contenu numérique de même qualité pédagogique que votre contenu classique
